- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn
Séminaire
Le 14 décembre 2023
Doron Grossman (Ladhyx, École Polytechnique)
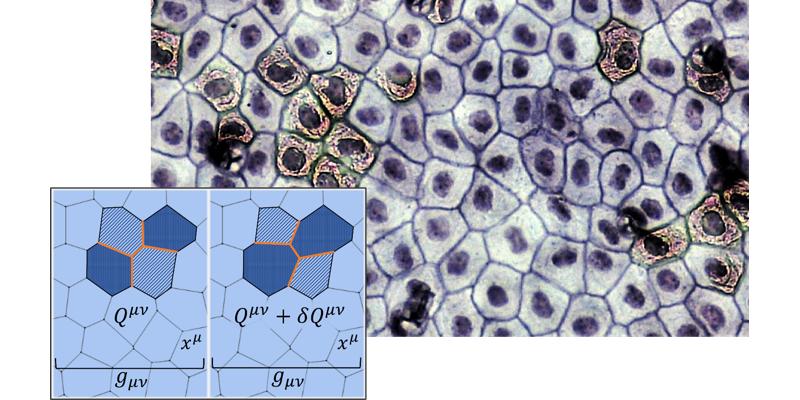
We present a covariant continuum formulation of a generalized two-dimensional vertexlike model of epithelial tissues which describes tissues with different underlying geometries, and allows for an analytical macroscopic description. Using a geometrical approach and out-of-equilibrium statistical mechanics, we calculate both mechanical and dynamical instabilities of a tissue, and their dependencies on various variables, including activity, and cell-shape heterogeneity (disorder). We show how both plastic cellular rearrangements and the tissue elastic response depend on the existence of mechanical residual stresses at the cellular level. Even freely growing tissues may exhibit a growth instability depending on the intrinsic proliferation rate. Our main result is an explicit calculation of the cell pressure in a homeostatic state of a confined growing tissue. We show that the homeostatic pressure can be negative and depends on the existence of mechanical residual stresses. This geometric model allows us to sort out elastic and plastic effects in a growing, flowing, tissue. We calculate the rheological response of such a living tissue, and show that it can exhibit shear thinning, shear thickening and thixotropic behaviour, depending on the conditions.
Contact: Philippe Marmottant
Date
14:00
Localisation
LIPhy, salle de conférence
- Imprimer
- Partager
- Partager sur Facebook
- Partager sur X
- Partager sur LinkedIn