Why use an optical cavity (of high finesse)?

Principle of detection by absorption spectroscopy

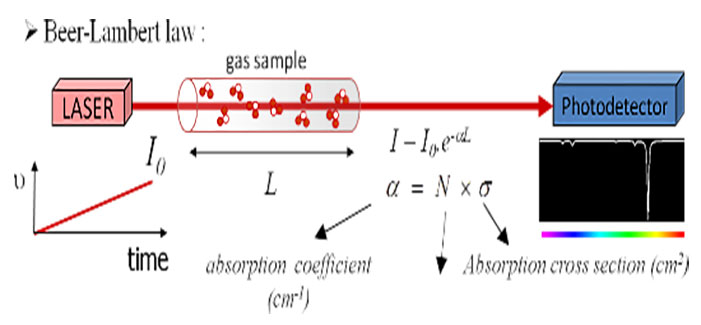
To measure absorption lines of molecules in a cell by absorption spectroscopy, we use the fact that incident light I0 decreases exponentially with the length L of interaction which is described by the Beer-Lambert law as :

I(ν)=I₀exp(-α(ν)L)
 

with a(ν) = Nσ(ν) where N is the concentration of the absorbing molecules and σ is the effective absorption cross section of that molecule at frequency ν.
If the effective absorption cross sections are known, the concentration of the absorbing molecules can be determined and, conversely, if the concentration of the absorbing molecules is known, the effective absorption cross sections can be determined. However, for small absorptions, it is not possible to distinguish the decay of the light intensity due to absorption in the cell from the measurement noise. In order to detect very small absorptions, one way is to increase the interaction length.

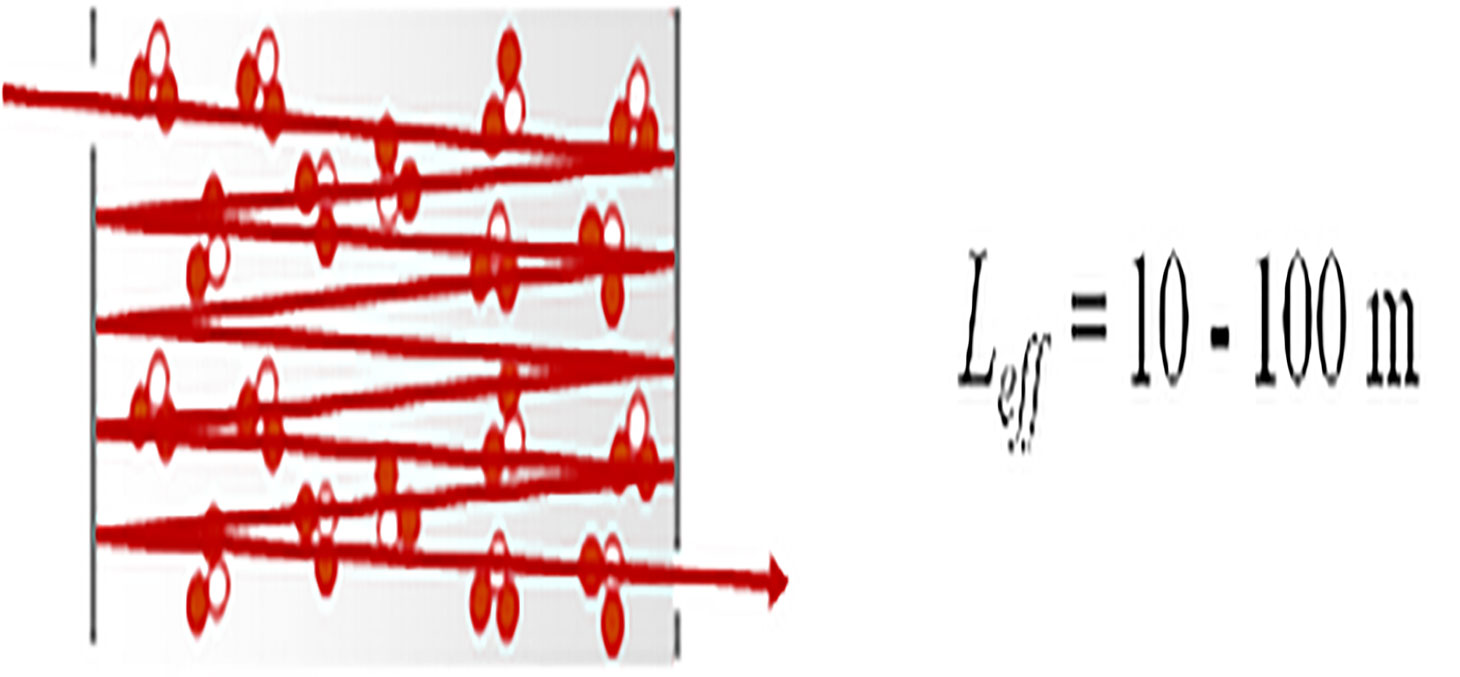
To increase the interaction length, a first thing we can do is to use multi-pass cells. One can have up to a hundred passes. We then obtain interaction lengths of up to 100 m for an absorption cell of 1 m.

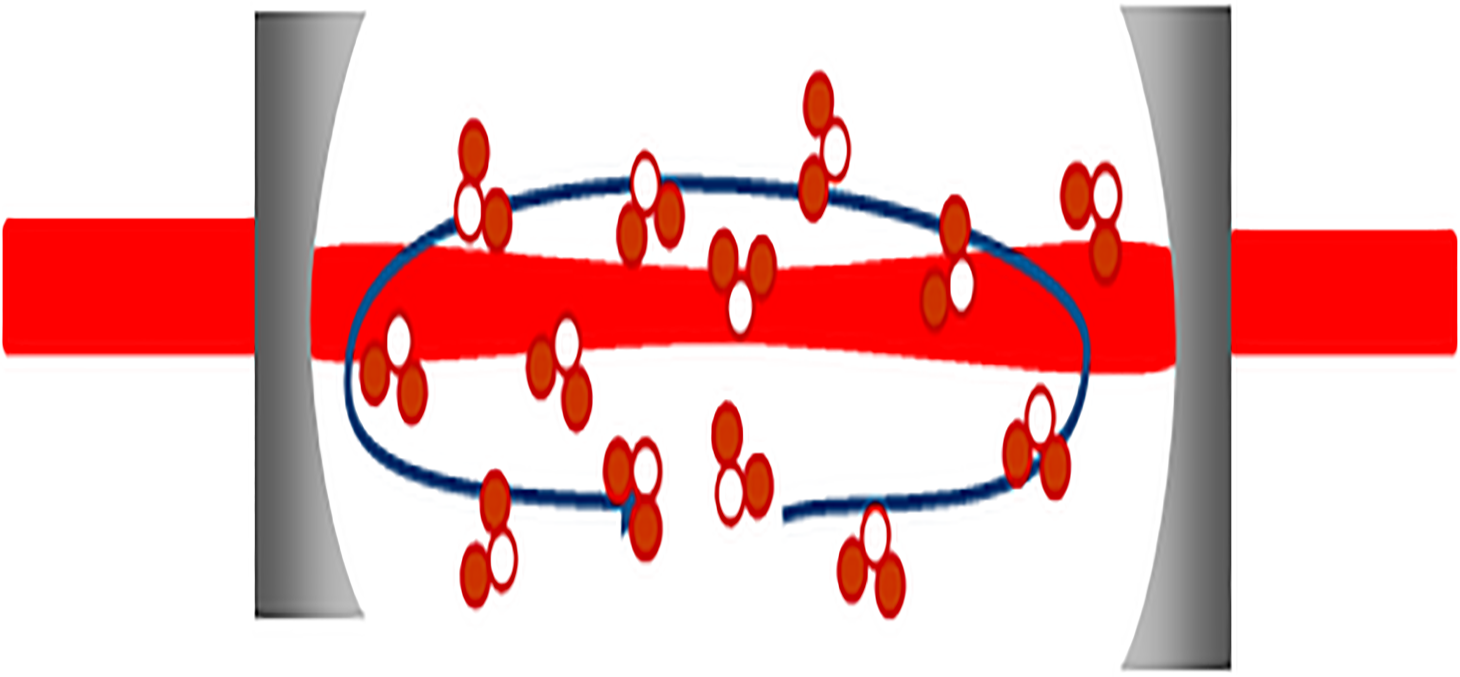
With high finesse optical cavities and high reflectivity mirrors, interaction lengths exceeding 10 km can be reached. Moreover, the volume of gas to probe is much smaller (100 times less). The effective interaction length Leff is then multiplied by the factor 2F/π, where F is the fineness of the cavity and depends on the reflection coefficient of the mirrors :

F = πR / 1-R

where R is the reflection coefficient of the mirrors.

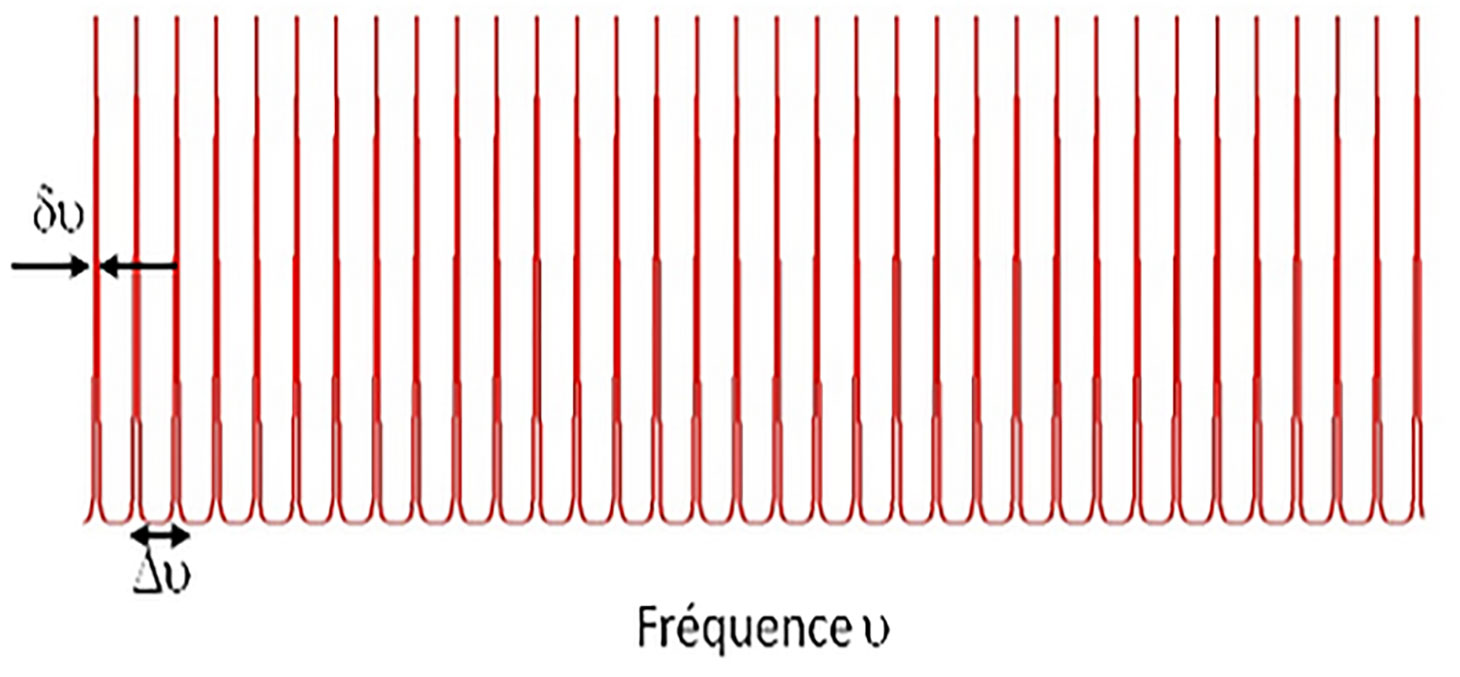
Since the wave is spatially limited, all frequencies are no longer transmitted through the cavity, only the resonant modes are transmitted. The wavelengths transmitted by the cavity are such that 2L = Nλ, where N is an integer. The frequencies are then separated by :

Δν = c/2L.

We find here the notion of sharpness. The fineness of the transmitted peaks increases with the reflection coefficient of the mirrors. Indeed, we can also define the fineness of the cavity by the ratio between the spacing between two consecutive modes and the width at half-height of a mode.

F = Δν / δν

The higher the reflection coefficient of the mirrors, the finer the transmitted modes will be, the fineness of the cavity will be high and the interaction path long.